policy gradient reinforcement learning illustration

Podcast: Play in new window | Download | Embed

LM101-063: How to Transform a Supervised Learning Machine into a Policy Gradient Reinforcement Learning Machine

Episode Summary:

This 63^rd episode of Learning Machines 101 discusses how to build reinforcement learning machines which become smarter with experience but do not use this acquired knowledge to modify their actions and behaviors. This episode explains how to build reinforcement learning machines whose behavior evolves as the learning machines become increasingly smarter. The essential idea for the construction of such reinforcement learning machines is based upon first developing a supervised learning machine. The supervised learning machine then “guesses” the desired response and updates its parameters using its guess for the desired response! Although the reasoning seems circular, this approach in fact is a variation of the important widely used machine learning method of Expectation-Maximization. Some applications to learning to play video games, control walking robots, and developing optimal trading strategies for the stock market are briefly mentioned as well.

Show Notes:

Hello everyone! Welcome to the sixtieth-third podcast in the podcast series Learning Machines 101. In this series of podcasts my goal is to discuss important concepts of artificial intelligence and machine learning in hopefully an entertaining and educational manner. Episode 62 explained how to build reinforcement learning machines which become smarter with experience but do not use this acquired knowledge to modify their actions and behaviors. This episode explains how to build reinforcement learning machines whose behavior evolves as the learning machines become increasingly smarter. Some applications to learning to play video games, control walking robots, and developing optimal trading strategies for the stock market are briefly mentioned as well.

In supervised learning, the learning machine is provided with explicit information regarding the correct response for a given input pattern. In unsupervised learning, the learning machine is simply provided input patterns without any explicit feedback from the environment. Reinforcement learning is an interesting combination of unsupervised and supervised learning methods which corresponds to the case where the learning machine interacts with its environment and the environment provides occasional minimal feedback regarding how the learning machine is performing without providing the learning machine with information regarding the correct response for a given environmental event. Reinforcement learning algorithms have been discussed in this podcast series in Episodes 2, 48, 49, 59, 61, 62 which can be found on the official website for Learning Machines 101: www.learningmachines101.com.

In Episode 62 we revised the concept of a supervised learning machine and showed how to transform a supervised learning machine into a Value Function Reinforcement Learning machine. The Value Function Reinforcement Learning machine is based upon the idea that the learning machine can examine a particular environmental state and predict the expected total amount of reinforcement it is expected to receive if that environmental state was obtained. In Episode 62, the focus was on “off-policy reinforcement learning” which means that the learning machine explores its statistical environment in order to acquire knowledge regarding the consequences of particular actions in its environment but the learning machine does not use this acquired knowledge to guide its behavior in the environment during the learning process. Presumably, after the learning process has been completed, this knowledge would then be incorporated into the learning machine’s strategies for generating actions. In this episode, we show how to construct a “policy gradient reinforcement learning machine” from a supervised learning machine which alters its statistical environment during the learning process. This type of policy gradient reinforcement learning machine illustrates the concept of “on-policy reinforcement learning”.

This type of learning process is fundamentally different in a fascinating way because both the learning machine and environment “co-construct” the learning machine’s experiences. In particular, the probability of a particular sequence of observed environmental states generated by the environment and actions generated by the learning machine has a probability distribution which will actually change as the learning machine acquires experience of its probabilistic environment. More specifically, the learning process for a learning machine corresponds to the adjustment of the learning machine’s “parameter values”. Different choices of parameters of the learning machine correspond to different behavioral strategies. The goal of the learning process is for the learning machine to discover a good set of parameter values.

In classical supervised or unsupervised learning paradigms, the statistical environment generates training stimuli for the learning machine. The behavior of the learning machine does not modify the probability that one training stimulus versus another will be presented. In a reinforcement learning paradigm, the results of the interactions of the environment and the learning machine influence the probability that a particular environmental event will be observed. Given a particular state of the environment, the learning machine executes an action which changes the state of the environment. The resulting sequence of environmental states depends upon the learning machine’s behaviors and indirectly upon the learning machine’s parameters. As the learning machine’s parameters are updated, the learning machine’s behavior is modified which implies the probability distribution of events in the learning machine’s environment will also change!

For example, consider the problem of trying to land a spacecraft on the moon. The state of the spacecraft has a particular height and velocity above the lunar surface. The acceleration towards the moon at a particular moment in time depends upon the thrust generated by the craft as well as the gravitational pull of the spacecraft towards the moon. Each time thrust is applied, this generates a different environmental state. In a supervised learning paradigm, one might train the spacecraft to generate a particular action for a given situation characterized by the spacecraft’s current height, velocity, and acceleration. In an unsupervised learning paradigm, the learning machine might simply “watch” an experienced pilot land the spacecraft multiple times but only the sequence of environmental states associated with a good landing would be experienced by the learning machine and the learning machine would not explicitly observe the actions of the experienced pilot. In both of these cases, the behavior of the learning machine’s statistical environment is functionally independent of the learning machine’s behavior as it acquires expertise during the learning process.

In contrast, an on-policy reinforcement learning machine has particular parameters which specify its behavior. When faced with a particular situation in its environment corresponding to an acceleration towards the lunar surface at a particular moment in time, the lunar lander learning machine will decide whether or not to apply its thrusters based upon its current parameter values. A direct consequence of this decision is the next state of the environment experienced by the lunar lander learning machine. Thus, the probability that the lunar lander experiences a particular environmental event depends not only upon the previous environmental event but also upon the lunar lander’s parameters.

Pong was one of the first video games ever invented and was released in 1972. It basically is a highly simplified version of ping-pong. Each of the two opponents have a paddle which moves in only one-dimension: Either up or down. In addition, there is a ping-pong ball which goes across the screen. You try to prevent the ball from going past you by moving your paddle up and down to block the ball and then the ball bounces off your paddle towards your opponent who tries to move her paddle up or down to block the ball. Andrej Karpathy in his May 2016 blog titled “Deep Reinforcement Learning: Pong from Pixels” gives a useful introductory review of policy gradient reinforcement learning methods of the type described here.

You can watch a Deep Learning Neural Network learn to play Pong on YouTube which was posted by Andrej Karpathy. I have provided the link to the YouTube channel in the show notes of this episode of learning machines 101 at: www.learningmachines101.com. The method is based upon the policy gradient method described here and discussed further in Karpathy’s blog.

The video tells a compelling story. You see the artificial neural network feebly move the paddle up and down while it misses many ping pong balls. But as the neural network acquires more experience, it manages to block more ping pong balls. And with large amounts of experience, the neural network plays like a world-class champion who has the both lighting fast reflexes as well as the ability to anticipate the ping pong balls trajectory!
It’s also important to note that the state of the environment is simply a collection of pixels.

Policy gradient reinforcement learning algorithms have also been applied for the purpose of teaching both two-legged and four-legged robots to learn to walk from experience. The reinforcement learning signal is a scalar measure of the “stability” of the robot and the parameters of the robot are adjusted so that the robot can successfully walk on a variety of surfaces. These parameters are updated in real-time so it can adapt to its walking environment. References to these papers are provided in the show notes of this 63^rd episode of Learning Machines 101 at: www.learningmachines101.com

Finally, a recent paper which appeared in arXiv covers the use of deep reinforcement learning using policy gradient reinforcement methods for the purpose of stock market portfolio management. In particular, the article discusses the problem of allocating an amount of money into different financial investments and focusses upon “cryptocurrencies” such as BitCoin as alternatives to government-issued money. A policy gradient reinforcement learning algorithm is used where the reinforcement signal is the total amount of money received over trading periods. This reference is also provided in the show notes of this episode!

So how can one design an on-policy reinforcement learning machine? We will begin with the idea that the learning machine’s statistical environment consists of a collection of independent and identically distributed “episodes”. The first environmental state of each episode occurs with some probability which is not dependent upon the parameters of the learning machine. However, the second, third, and all subsequent environmental states of each episode will depend upon the parameters of the learning machine. Thus, the probability the learning machine experiences a particular episode is functionally dependent upon the current parameter values of the learning machine. More specifically, it is assumed that the probability of generating an action given the current environmental state depends upon the learning machine’s parameter values.

Assume that the reinforcement penalty received by the learning machine when it experiences an episode can be explicitly calculated by the sequence of environmental states experienced by the learning machine in that episode. The goal of the learning process is then defined as minimizing the expected episode reinforcement penalty.

An empirical approximation to the expected episode reinforcement penalty for the learning machine’s current parameter values can be generated using the following methodology. First, the environment randomly generates an initial state. Second, the learning machine randomly generates an action with some probability based upon its current parameter values and the current state of the environment. Third, the environment randomly generates a new state based upon the previous state of the environment and the learning machine’s action. This process continues until the episode is complete. An approximation to the expected episode reinforcement penalty given the machine’s current parameter values is then obtained by computing the reinforcement penalty for an episode which has been simulated using the learning machine’s current parameter values in this manner.

Similarly, this same technique can be used to estimate an approximation to the gradient of the expected reinforcement penalty. The true gradient of the expected reinforcement penalty for a given set of learning machine parameter values is calculated by computing the average value of the derivative of the probability of the episode multiplied by the reinforcement penalty calculated for that episode. We then use a result from calculus which says that the derivative of a probability is equal to the derivative of the natural logarithm of that probability multiplied by that probability. Thus, we can rewrite the true gradient of the expected reinforcement penalty for a given set of learning machine parameter values by computing the average value of the derivative of the logarithm of the probability of the episode multiplied by the reinforcement penalty for the episode and then multiplied by the probability of the episode. An approximation to the derivative of this conditional expectation is then obtained by first generating a simulated episode and then plugging that simulated episode into the formula for the reinforcement penalty for an episode multiplied by the derivative of the logarithm of the episode’s probability given the current learning machine’s parameter values.

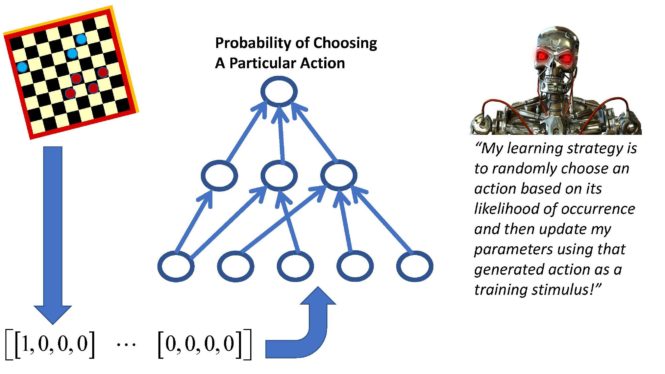
So the key idea is as follows. We start with a supervised learning machine which takes an environmental state and the learning machine’s current parameter values and then produces a probability for each possible action the learning machine could generate. Examples of such supervised learning machines would include logistic regression models, multinomial logistic regression models also known as linear softmax models, and multi-layer feedforward deep neural networks whose output layer consists of softmax units. In principle, if we knew the desired action for a given environmental state, then we could train the learning machine using a supervised learning algorithm so that it learns the desired probability of choosing a particular action given a particular environmental state input pattern. However, this is not a supervised learning problem because we do not know the desired response for a given input pattern.

So, instead, what we effectively do is we compute the learning machine’s probability distribution of possible actions for a given input environmental state, and then we use that probability distribution to pick one of those actions at random. That is, if the learning machine predicts action A will occur with probability P then we pick action A with probability P for the learning machine’s current parameter values. Then we use that action which was generated and the input pattern which generated that action as a “training stimulus”! In addition, we use a special objective function for learning which involves the derivative of the logarithm of the probability of P which was informally derived above. I know this sounds like circular reasoning but in fact this turns out to be a disguised version of a very important and very popular machine learning algorithm called the Expectation Maximization algorithm which was discussed in detail in Episode 22 of learning machines 101. In the statistics literature, such methods are referred to as Stochastic Approximation Expectation Maximization or Monte Carlo Expectation Maximization methods. The reference by Gu and Kong (1998) published in the Proceedings of the National Academy of Sciences or the reference in Sugiyama’s book on pages 96-98 in Section 7.2 provide a more detailed discussion of these issues. Also see the review article by Kushner (2009). All of these references can be found in the show notes of this episode of learning machines 101! Also Andre Karpathy in his May 2016 blog has a nice discussion of this approach as well. Ron Williams in 1992 was one of the earlier proponents of this approach within the context of deep learning neural networks.

So again, to summarize, since we don’t know the desired response for a given input pattern, the learning machine essentially guesses what the desired response should be and then uses that guess to adjust its parameter values!!! I want to emphasize again this is not a heuristic and one can prove rigorous mathematical theorems establishing that this type of procedure will work!!! I have provided some references to the relevant statistical literature at the end of this podcast at the website: www.learningmachines101.com.

Thank you again for listening to this episode of Learning Machines 101! I would like to remind you also that if you are a member of the Learning Machines 101 community, please update your user profile and let me know what topics you would like me to cover in this podcast.

You can update your user profile when you receive the email newsletter by simply clicking on the: “Let us know what you want to hear” link!

If you are not a member of the Learning Machines 101 community, you can join the community by visiting our website at: www.learningmachines101.com and you will have the opportunity to update your user profile at that time. You can also post requests for specific topics or comments about the show in the Statistical Machine Learning Forum on Linked In.

From time to time, I will review the profiles of members of the Learning Machines 101 community and comments posted in the Statistical Machine Learning Forum on Linked In and do my best to talk about topics of interest to the members of this group!

And don’t forget to follow us on TWITTER. The twitter handle for Learning Machines 101 is “lm101talk”!

Also please visit us on ITUNES and leave a review. You can do this by going to the website: www.learningmachines101.com and then clicking on the ITUNES icon. This will be very helpful to this podcast! Thank you so much. Your feedback and encouragement are greatly valued!

Keywords: Reinforcement Learning, Policy Gradient Reinforcement Learning, Expectation Maximization, Supervised Learning

LM101-063: How to Transform a Supervised Learning Machine into a Policy Gradient Reinforcement Learning Machine

LM101-063: How to Transform a Supervised Learning Machine into a Policy Gradient Reinforcement Learning Machine

Episode Summary:

Show Notes:

Further Reading and Videos:

Leave a Reply Cancel reply